On pourrait penser que calculer la performance (que nous appelerons aussi rendement) d’un portefeuille est chose triviale. Pas tant que cela : il y a des méthodes aberrantes et plusieurs méthodes pertinentes.
Cas simple, sans apport intermédiaire.
Le seul cas simple est celui où il n’y a qu’un seul apport au portefeuille, l’apport initial. Alors la performance est la différence relative entre le capital final et initial :
r = (Cf – F0) / F0
où :
- F0 = apport initial au temps 0,
- Cf = capital final au temps T,
- r = performance.
Cette performance est la performance période, c’est-à-dire la performance sur l’ensemble de la période T. Pour le ramener à une performance annuelle R1 c’est-à-dire sur un temps T1 = 1 an, il faut l’annualiser, ce qui par définition revient à utiliser la relation fondamentale
(1+R1)^(1/T1) = (1+r)^(1/T) (a)
ce qui donne pour calculer R1 :
R1 = (1+r)^(T1/T) – 1
Un rendement est associé à une durée, et on passe d’une durée à une autre par la relation (a). A partir de maintenant, la performance ou le rendement sans autre précision désigneront la performance période.
Notons une autre autre relation fondamentale. Une somme initiale F0 placée à ce rendement devient après un temps t la somme :
Ft = F0 * (1+r)^(t/T) = F0 * (1+R1)^(t/T1)
Exemple. Au 1er juillet 2012 mon portefeuille a une valeur de 5.000 €, au 1er mai 2013 il a une valeur de 5.738 €. Sa performance période est donc r = (5.738 – 5.000) / 5.000 = 14,76 %. Sa performance annualisée est R1 = (1+0,1476)^(12 mois /10 mois) – 1 = 17,96 %. Si la performance continue à ce rythme, au 31 décembre 2013 mon portefeuille vaudra 5.000*(1+0,1476)^(18 mois /10 mois) = 6.406 €.
Quand tout se complique
Avec des apports (ou des retraits) intermédiaires tout devient plus complexe. Il y a même des méthodes aberrantes. C’est le cas de la première qui vienne à l’esprit, en définissant encore la performance comme la différence entre le capital final moins le capital initial, divisé par le capital initial. Imaginons par exemple la situation suivante :
- t0 : je mets 100 € dans le portefeuille
- t1 : la valorisation n’a pas changé. Je rajoute 100 €.
- t2 : la valorisation n’a toujours pas changé.
Avec la définition proposée on trouve que la performance est (200 – 100) / 100 soit 100%, absurde puisque je n’ai pas gagné d’argent.
Moins absurde semblerait être de faire la différence entre le capital final moins le capital total apporté, divisé par le capital total apporté. Dans l’exemple précédent on trouverait une performance de (200 – 200) / 200 = 0% comme il se doit. Mais dans la situation suivante :
- t0 : je mets 100 € dans le portefeuille
- t1 : la valorisation monte de 10%. Je retire 99 €. Le portefeuille vaut 11 €.
- t2 : la valorisation n’a pas changé.
Avec la définition proposée on trouve que la performance est (11-1)/1 = 1.000 % ce qui n’est pas beaucoup plus raisonnable que la solution précédente. Cela donne des solutions absurdes car nous n’avons pas fait intervenir le temps dans les calculs c’est-a-dire le fait que les capitaux apportés ne travaillent pas sur la même durée.
Calcul avec des apports intermédiaires
Dans le cas général il y a essentiellement deux façons de calculer une performance : la performance de la part et la performance globale du portefeuille. Nous nous proposons de définir ce deux approches et d’examiner comment on les calcule.
A. Deux ratios de performance
1. La performance de la part. En français cela s’appelle aussi le Taux de Rentabilité Pondéré par le Temps (TRPT). En anglais Time Weighted Rate of Return(TWRR). Le TRPT comptabilise :
- la performance d’un panel d’actions,
- le gain fait par des prises de plus-values à cours élevé et rachat à cours bas
mais ne prend pas en compte l’apport de performance permis par des entrées d’argent sur le portefeuille lorsque les cours sont bas. C’est la performance dont la publication est rendue obligatoire pour les gérants d’OPCM car on ne souhaite pas juger la performance d’un gérant sur le moment où les épargnants choisissent de souscrire ou racheter leurs parts d’OPCVM. C’est aussi la méthode requise quand entrent ou sortent des membres dans un club d’investissement.
2. La performance globale du portefeuille. En français cela s’appelle aussi le Taux de Retour Interne (TRI), le taux actuarial, le taux effectif de rendement, le taux de rendement actuarial, etc. En anglais Internal Rate of Return (IRR). Ce taux comptabilise les apports au portefeuille et mesure donc la performance du gérant qui maitrise les flux de capitaux. Cela peut être le cas de certains investisseurs particuliers.
Exemple. Imaginons le résultat suivant sur une période donnée
- Rendement de la part : +12 %
- TRI : +10 %
- Indice de référence : +11 %
Cela signifie que :
- Part > indice : les valeurs choisies ont mieux performé que l’indice de référence.
- TRI < indice : les apports ont été faits aux mauvais moments, c’est-à-dire sur valeurs de part élevées.
Il est en effet clair que si vous apportez du capital lorsque la part a une faible valorisation vous gagnerez plus qu’en apportant ce capital sur une part mieux valorisée.
B. Définitions mathématiques
Les ratios reposent tous les deux sur le découpage du temps en n périodes séparées par les apports ou les retraits du portefeuille. Notations : Au temps t0=0 le capital initial C0 est nul, on fait un apport en capital (flux) F0. Du fait des bénéfices ou pertes, au temps t1 le capital est devenu C1, différent de C0. De façon générale, au temps ti (i=1,2,…,n-1), le capital est devenu Ci, on apporte alors Fi (si Fi<0 il s’agit d’un retrait). Immédiatement après le temps ti le capital est donc Ci+Fi. Au temps final T=tn le capital final est Cf.
ri = ( Ci – C(i-1) – F(i-1) ) / ( C(i-1)+F(i-1) )
Le TRPT est défini comme le rendement composé :
TRPT = (1+r1)*(1+r2)*(1+r3)*…*(1+
2. Définition du TRI (performance du portefeuille). L’apport Fi travaille pendant un temps (T-ti), s’il travaille avec un rendement r il devient au temps T la somme Fi * (1+r)^(T-ti)/T. Si tous les apports travaillent avec ce taux alors au temps T on doit avoir le capital :
Cf = somme(i=0 à n) Fi * (1+r)^(T-ti)/T. (2)
Le TRI est défini comme un nombre r solution de cette équation. Il est ausi souvent présenté (c’est équivalent) comme une solution de l’équation :
somme(i=0 à n) Fi / (1+TRI)^ti/T – Cf / (1+TRI) = 0. (3)
C’est donc le rendement défini par le fait que si tous les apports travaillent avec ce même rendement alors on obtient le capital final.
C. Calcul pratique.
1. TRPT. On peut appliquer la relation (1). Mais le procédé le plus courant pour calculer le TRPT est de raisonner en parts :
- Au départ on divise le portefeuille en un nombre arbitraire de parts, souvent choisi de telle sorte que la valeur initiale de la part soit 1 ou 100.
- Tant qu’il n’y a pas d’apport ou de retrait dans le portefeuille, la valeur de la part est donnée par la valeur du portefeuille (qui, elle, fluctue) divisé par le nombre de parts,
- Lors d’un apport ou de retrait, on augmente ou diminue le nombre de parts de telle sorte que la valeur de la part reste constante. Exemple j’ai 10 parts a 100 € soit 1000 € dans mon portefeuille et j’apporte 250 € (donc = 2,5 parts). Après apport le portefeuille compte donc 12,5 part a 100 € soit 1250 euros.
- Ensuite, la valeur de la part recommence à fluctuer en fonction du marché.
- La performance du portefeuille en % est la valeur de la part divisée par la valeur initiale de la part, moins un.
- Bien sûr cette façon de faire donne le même résultat que la relation (1).
2.TRI. Le calcul du TRI est plus complexe parce que la relation (3) a plusieurs solutions et qu’elle ne peut être résolue que par approximations successives. Heureusement elle est préprogrammée dans OpenOffice Classeur (ou Excel) sous la dénomination TRI.PAIEMENTS (la fonction de base TRI ne fonctionne que pour des apports à intervalles constants) avec la syntaxe TRI.PAIEMENTS(F0:Fn;t0:tn;esti
3. Approximation de TRI ou Taux de Rentabilité Pondéré par le Capital (TRPC) ou Taux de Retour Pondéré par les Capitaux Investis (TRPCI). En anglais j’ai l’impression que cela s’appelle Money Weighted Rate of Return (MWRR) ou Total Return Rate (TRR). Si on suppose que le TRI est petit et que les flux initiaux ne sont pas trop grands devant les flux finaux alors en développant la relation (2) linéairement on trouve que le TRI est proche de
TRPC = (Cf – somme(i=0 à n) Fi ) / somme(i=0 à n) (T-ti)*Fi / T (4)
Au numérateur on reconnaît le bénéfice net : c’est la somme réellement gagnée ou perdue, au dénominateur ce que l’on appelle capital employé. Ce dernier est la somme des apports de capitaux chacun étant pondéré par le temps passé à travailler. Cette valeur peut être utilisée pour la variable estimation de la fonction TRI.PAIEMENTS.
D. Exemples
Exemple 1. Considérons le cas suivant :
- t0 : je mets 100 € dans le portefeuille. La part est a 100 €.
- t1 : la valeur du portefeuille est montée de 10 % à 110 €. Je rajoute du capital pour une part soit 110 €.
- t2 : la valeur du portefeuille redescend de 9,09 % pour arriver à 200 €.
Il y a toujours 2 parts dont la valeur est de 100 €, la performance de la part est nulle. J’ai injecté 210 € et ai maintenant 200 €, j’ai donc perdu 10 €. Le TRI est donc négatif. Pour le calculer il faut avoir les valeurs des ti ; en prenant t0 = 0, t1 = 365, t2 = 730 je trouve TRI(excel) = -3,26 % par an soit TRI = (1-0,0326)^2-1 = -6,41 % sur les deux ans.
Exemple 2. A l’inverse, en apportant du capital à un point bas de la part :
- t0 : je mets 100 € dans le portefeuille. La part est a 100 €.
- t1 : la valeur du portefeuille a baissé de 10 % soit 90 €. Je rajoute du capital pour une part soit 90 €.
- t2 : la valeur du portefeuille remonte de 11,11 % pour arriver à 200 €.
La performance de la part est nulle et j’ai gagné 10 €. En prenant t0 = 0, t1 = 365, t2 = 730 je trouve TRI(excel) = +3,41 % par an soit TRI = +6,93 % sur les deux ans.
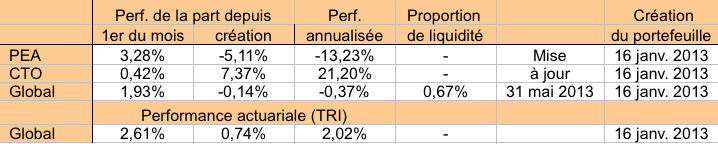
Exemple 3. Le tableau suivant montre un cas réel. On voit notamment que la performance de la part peut être négative (-0,14%) alors que l’on a gagné de l’argent (TRI=0,74%>0) : c’est parce que l’on a investi plus d’argent quand la part était basse que lorsqu’elle était haute.
Références
- http://gestion.coursgratuits.
net/economie/retours-et-taux- d-investissements.php - http://en.wikipedia.org/wiki/
Internal_rate_of_return - http://en.wikipedia.org/wiki/
True_Time-Weighted_Rate_of_ Return - Une discussion sur le sujet : http://www.devenir-rentier.fr/
viewtopic.php?pid=63058#p63058 , notamment les posts de Chroom et Julien. - TWR : http://moneystore.be/2012/
gestion/calculer-performance- dun-portefeuille - TRPC : http://jybaudot.fr/Banque/
rentpond.html - Notice de la fonction TRI : http://office.microsoft.com/
fr-fr/excel-help/tri- paiements-HP005209341.aspx - Considérations générales et très particulières, voir notamment p. 227 : http://www.actuaries.org/AFIR/
Colloquia/Paris/Lam.pdf - Livres de mathématiques financières.

Bonjour,
Merci pour la page qui est intéressante (http://valeurbourse.com/2013/06/calculer-la-performance-de-son-portefeuille/). Même bravo car votre page est claire alors qu’on parle de mathématiques! En revanche, le tableau de l’exemple 3 du paragraphe D ne s’affiche pas. Ce qui est dommage car on ne peut pas vérifier si l’on a bien compris. Dés que vous avez du temps, pourriez- vous y remédier svp?
Merci et encore bravo
LP
Bonsoir Pouillini,
désolé de vous répondre tardivement, mais la correction a été apportée. Merci pour votre remarque et l’intérêt que vous portez à notre blog.
Bonne soirée.
Bonjour,
nous avons enfin réussi à afficher le tableau, désolé pour ce retard.
N’hésitez pas à nous faire des commentaires, à nous demander des éclaircissements sur ce sujet pas si simple, nous avons conscience que cet article peut-être amélioré et c’est avec plaisir que nous le ferons en fonction de vos questions.
JL
Bonjour,
Merci pour cet article très didactique sur un sujet complexe.
Des questions très pratiques concernant le calcul de la valeur de la part d’un portefeuille : à t = 0, faut-il inclure les sommes du compte espèces qui lui est associé (cas du PEA par exemple) ? Les dividendes versés ultérieurement sur le compte espèces sont-ils considérés, ou non, comme une diminution du nombre de parts portefeuille ? Les achats ou ventes impliquant le seul compte espèces sont-ils considérés ou non comme des apports / retraits de parts du portefeuille ?
Merci vivement des précisions que vous voudrez bien m’apporter.
Cordialement.
Serge
Bonjour Serge,
pour ma part je comptabilise les espèces du compte dès le début. Ensuite, les dividendes faisant partie de la performance, il ne faut pas les considérer comme des apports; il n’y a donc aucun traitement à effectuer. Il en est de même pour les achats et les ventes.
En revanche, tout retrait ou apport nécessite un nouveau calcul du nombre de parts (le prix de la part devant rester identique).
J’espère avoir répondu à vos questions.
Bonnes plus-values,
Boris
Bonjour,
Pour calculer, comme vous le soulignez dans votre réponse, le nombre de parts correspondant à un mouvement externe (retrait ou apport) le jour J, il faut en principe déterminer la valeur de la part le jour J-1 précédent et ceci suppose de connaître la valeur liquidative du portefeuille à J-1, ce qui n’est pas indiqué sur les relevés des courtiers. Ou alors il faut relever quotidiennement la valeur liquidative en fin de journée, ce qui est astreignant.
Soit un exemple chiffré simple :
01/01/2015 : valeur du portefeuille : 15000 soit 100 parts de 150 €
10/01/2015 : retrait 3000 €
20/01/2015 : apport 1000 €
31/01/2015 : valeur du portefeuille : 14000 €
Comment concrètement calculez vous le nombre de parts correpondant au retrait de 2000 € , puis à l’apport de 1000 €,
notamment si vous ne connaissez pas la VL le 09/01/2016 et le 19/01/2015 (cas le plus fréquent a priori) ?
Je vous remercie très vivement de bien vouloir m’éclairer sur la façon d’effectuer ces calculs.
Cordialement.
Serge
Bonjour,
Votre exemple n°2 donne un TRI de 6,93% pourtant vous avez gagné 10€ avec un investissement de 190€. Ce qui nous donne 10undefined190 = 5,26%
Je n'ai donc pas l'impression que le TRI représente le vrai rendement.
Bonjour Arthur,
dans votre approche vous considérez que les 190 € ont « travaillé » sur une même période. Ce qui est faux, puisque 100 € ont travaillé sur deux ans, et 90 € ont travaillé sur un an.
Le TRI permet justement de calculer précisément la performance ramenée au temps réellement travaillé.
Bonjour,
Connaissez-vous des logiciels ou des sites web ou encore des templates Open Office qui permettent de facilement simuler la performance de portefeuilles ?
Personnellement j'ai simulé votre exemple D.2 avec le logiciel Sweet Bourse et avec le portefeuille virtuel de Investir.lesechos et voici ce que j'obtiens :
J'ai simulé un apport de 99.5 euros le 27 aout 2019 et l'achat immédiat de 10 actions Mercialys à 9.95 puis le 27 aout 2020 un nouvel apport de 89.5 euros pour acheter à nouveau 10 actions à 8.95. Celle-ci valant environ 9.95 le 27 aout 2021, on est à peu près dans le cas présenté. Le portefeuille virtuel de Investir ne m'indique que la performance basique à savoir gainundefinedapport (5.05%) et le le logiciel sweet bourse apporte 2 informations supplémentaires (rendement annuel et performance équivalente qui semble être le rendement sur la durée totale soit 2 ans) . Le résultat s'approche bien de vos valeurs (resp. 3.12 et 6.34 % contre 3.41 et 6.93 % pour vous).
Il semble donc que seul Sweet Bourse donne les réelles indications mais je ne trouve pas ce logiciel très facile d'utilisation donc si vous avez d'autres références…
Bonjour Chris, désolé pour ma réponse tardive, je n’ai pas été notifié de votre commentaire.
Pour le suivi de mon portefeuille, je n’utilise aucun logiciel du marché, car j’ai créé mon propre logiciel. Et il est très bien :-).
Avez-vous regardé ce que propose zonebourse ? Ca a l’air bien.
Bonjour,
j'ai adoré l'article qui est bien écrit et qui donne des exemples parlant.
Ce qui m'aiderait serait les tableaux Excel avec les formules pour les exemples 1 et 2 🙂
Merci et bon courage